NAND gate

NAND gate truth table
Input		Output
A	B	A NAND B
0	0	1
0	1	1
1	0	1
1	1	0

In digital electronics, a NAND gate is a logic gate which produces an output of false when all its inputs are true; thus the outputs are the complement of the AND gate. A LOW (0) output results only if all the inputs to the gate are HIGH (1); if any input is LOW (0), a HIGH (1) output results.

The NAND gate is significant because any Boolean function can be implemented by using a combination of NAND gates. This property is called "functional completeness". It shares this property with the NOR gate. Digital systems employing certain logic circuits take advantage of NAND's functional completeness.

A two-input NAND gate can be expressed in Boolean logic as ${\overline {A\cdot B}}={\overline {A}}+{\overline {B}}$.

Functional completeness

Construction of a NAND gate from four NOR gates.

Main articles: NAND logic and NOR logic

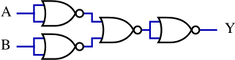
The NAND gate has the property of functional completeness, which it shares with the NOR gate. That is, any other logic function (AND, OR, etc.) can be implemented using only NAND gates.

As NOR gates are also functionally complete, if no specific NAND gates are available, one can be made from NOR gates using NOR logic.