XOR gate: Difference between revisions
(Created page with "{| class="wikitable floatright" style="text-align:center" |- ! colspan="3" | XOR gate truth table |- bgcolor="#ddeeff" |colspan=2|'''Input''' || '''Output''' |- bgcolor="#ddeeff" | A || B || A XOR B |- |{{no2|0}} || {{no2|0}} || {{no2|0}} |- |{{no2|0}} || {{yes2|1}} || {{yes2|1}} |- |{{yes2|1}} || {{no2|0}} || {{yes2|1}} |- |{{yes2|1}} || {{yes2|1}} || {{no2|0}} |} In digital electronics, an '''XOR gate''' is a logic gate which produces an output of true when...") |
m (→See also) |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 15: | Line 15: | ||
|{{yes2|1}} || {{yes2|1}} || {{no2|0}} | |{{yes2|1}} || {{yes2|1}} || {{no2|0}} | ||
|} | |} | ||
In [[digital electronics]], an '''XOR gate''' is a [[logic gate]] which produces an output of true when any of its inputs are true, but not both. A LOW (0) output results when all of the inputs to the gate are LOW or all of the inputs are HIGH (1); if any of the inputs are HIGH | [[File:XOR ANSI.svg|thumb|152x152px|ANSI XOR gate symbol]] | ||
In [[digital electronics]], an '''XOR gate''' or '''Exclusive OR''' is a [[logic gate]] which produces an output of true when any one of its inputs are true, but not both. A LOW (0) output results when all of the inputs to the gate are LOW or all of the inputs are HIGH (1); if any one of the inputs are HIGH, a HIGH output results. | |||
The XOR gate (along with the [[XNOR gate]]) is one of the only two logic gates that does not have an [[integrated circuit]] containing more than two inputs. | |||
== Logic == | == Logic == | ||
A two-input OR gate can be expressed in [[Boolean logic]] as <math>A \cdot \overline B + \overline A \cdot B</math>, <math>(A + B) \cdot (\overline A + \overline B)</math> or <math>A \oplus B</math>. | A two-input OR gate can be expressed in [[Boolean logic]] as <math>A \cdot \overline B + \overline A \cdot B</math>, <math>(A + B) \cdot (\overline A + \overline B)</math> or <math>A \oplus B</math>. | ||
= Alternatives = | |||
If a specific type of gate is not available, a circuit that implements the same function can be constructed from other available gates. Through the use of the "universal" [[NAND gate|NAND gates]] and [[NOR gate|NOR gates]], almost any other Boolean logic gate can be constructed. | |||
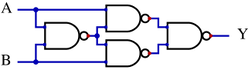
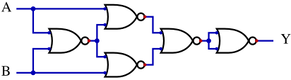
A XOR gate can be constructed using four NAND gates or five NOR gates in the following topologies: | |||
{| | |||
![[File:XOR from NAND ANSI.svg|248x248px]] | |||
![[File:XOR from NOR ANSI.svg|291x291px]] | |||
|} | |||
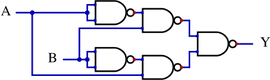
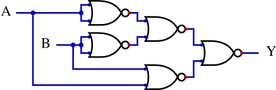
Additionally, using a different topology, the same can be achieved as follows: | |||
{| | |||
|[[File:XOR from NAND ASNI 2.svg|270x270px]] | |||
|[[File:XOR from NOR ANSI 2.svg|276x276px]] | |||
|} | |||
{{Stub}} | {{Stub}} | ||
| Line 26: | Line 43: | ||
* [[NAND gate]] | * [[NAND gate]] | ||
* [[NOR gate]] | * [[NOR gate]] | ||
* [[XNOR gate]] | * [[XNOR gate]] | ||
* [[Inverter|Inverter (NOT gate)]] | * [[Inverter|Inverter (NOT gate)]] | ||
Latest revision as of 06:18, 9 November 2023
| XOR gate truth table | ||
|---|---|---|
| Input | Output | |
| A | B | A XOR B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |

In digital electronics, an XOR gate or Exclusive OR is a logic gate which produces an output of true when any one of its inputs are true, but not both. A LOW (0) output results when all of the inputs to the gate are LOW or all of the inputs are HIGH (1); if any one of the inputs are HIGH, a HIGH output results.
The XOR gate (along with the XNOR gate) is one of the only two logic gates that does not have an integrated circuit containing more than two inputs.
Logic
A two-input OR gate can be expressed in Boolean logic as , or .
Alternatives
If a specific type of gate is not available, a circuit that implements the same function can be constructed from other available gates. Through the use of the "universal" NAND gates and NOR gates, almost any other Boolean logic gate can be constructed.
A XOR gate can be constructed using four NAND gates or five NOR gates in the following topologies:
|
|
|---|
Additionally, using a different topology, the same can be achieved as follows:
|
|


