NOR gate: Difference between revisions
mNo edit summary |
mNo edit summary |
||
| (One intermediate revision by the same user not shown) | |||
| Line 15: | Line 15: | ||
|{{yes2|1}} || {{yes2|1}} || {{no2|0}} | |{{yes2|1}} || {{yes2|1}} || {{no2|0}} | ||
|} | |} | ||
[[File:NOR ANSI.svg|thumb|165x165px|ANSI NOR gate symbol]] | |||
In [[digital electronics]], a '''NOR gate''', is a [[logic gate]] which produces true if all the inputs are false; thus the outputs are the complement of the OR gate. A HIGH output (1) results if both the inputs to the gate are LOW (0); if one or both input is HIGH (1), a LOW output (0) results. | In [[digital electronics]], a '''NOR gate''', is a [[logic gate]] which produces true if all the inputs are false; thus the outputs are the complement of the OR gate. A HIGH output (1) results if both the inputs to the gate are LOW (0); if one or both input is HIGH (1), a LOW output (0) results. | ||
| Line 22: | Line 23: | ||
The function NOR(a<sub>1</sub>, a<sub>2</sub>, ..., a<sub>''n''</sub>) is logically equivalent to NOT(a<sub>1</sub> OR a<sub>2</sub> OR ... OR a<sub>''n''</sub>). | The function NOR(a<sub>1</sub>, a<sub>2</sub>, ..., a<sub>''n''</sub>) is logically equivalent to NOT(a<sub>1</sub> OR a<sub>2</sub> OR ... OR a<sub>''n''</sub>). | ||
A two-input NOR gate can be expressed in Boolean logic as <math>\overline { A + B } = \overline A \cdot \overline B</math>. | A two-input NOR gate can be expressed in [[Boolean logic]] as <math>\overline { A + B } = \overline A \cdot \overline B</math>. | ||
Another way of expressing A NOR B is <math>\overline { A \lor B }</math>, where the symbol <math>\lor</math> signifies OR and the bar signifies the negation of the expression under it: in essence, simply <math>\neg(A \lor B)</math>. | Another way of expressing A NOR B is <math>\overline { A \lor B }</math>, where the symbol <math>\lor</math> signifies OR and the bar signifies the negation of the expression under it: in essence, simply <math>\neg(A \lor B)</math>. | ||
Latest revision as of 19:10, 8 November 2023
| NOR gate truth table | ||
|---|---|---|
| Input | Output | |
| A | B | A NOR B |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
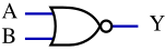
In digital electronics, a NOR gate, is a logic gate which produces true if all the inputs are false; thus the outputs are the complement of the OR gate. A HIGH output (1) results if both the inputs to the gate are LOW (0); if one or both input is HIGH (1), a LOW output (0) results.
The NOR gate is significant because any Boolean function can be implemented by using a combination of NOR gates. This property is called "functional completeness". It shares this property with the NAND gate. Digital systems employing certain logic circuits take advantage of NAND's functional completeness.
Logic
The function NOR(a1, a2, ..., an) is logically equivalent to NOT(a1 OR a2 OR ... OR an).
A two-input NOR gate can be expressed in Boolean logic as .
Another way of expressing A NOR B is , where the symbol signifies OR and the bar signifies the negation of the expression under it: in essence, simply .
Functional completeness
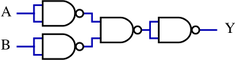
The NOR gate has the property of functional completeness, which it shares with the NAND gate. That is, any other logic function (AND, OR, etc.) can be implemented using only NOR gates.
As NAND gates are also functionally complete, if no specific NOR gates are available, one can be made from NAND gates using NAND logic.



